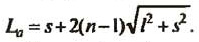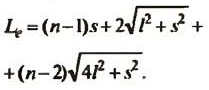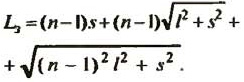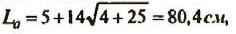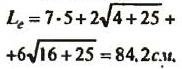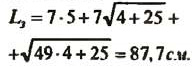Говорят, что настоящим математиком может считаться только тот, кто видит математические закономерности там, где их не замечает никто. Посмотрим, например, на ботиночные шнурки и попытаемся исследовать способы, которыми они завязаны. На этот важный вопрос серьезные исследователи почему-то долго не обращали внимания. Но осенью 1995 года в журнале «Mathematical Intelligencer» появилась статья сотрудника Университета северной Калифорнии Джона Халтона «Проблемы ботинкологии», которая этот пробел наконец-то восполнила.

Пять основных способов ботиночной шнуровки: американский зигзаг (1), европейский стандарт (2), шнуровка с запасом (3) и два вида канадской затяжки (4,5).

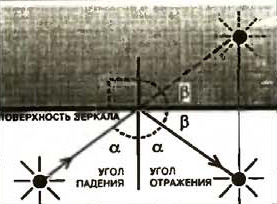
Принцип Ферма определяет один из основных законов геометрической оптики: угол падения светового луча на зеркало равен углу его отражения. Поэтому все симметричные отрезки перед зеркалом и в «Зазеркалье» имеют одинаковую длину.

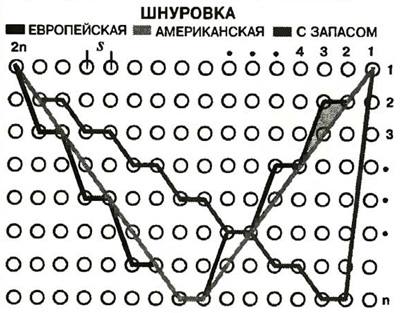
Полные диаграммы трех способов шнуровки. Нечетные столбцы соответствуют левому ряду отверстий, четные — правому. Расстояние между столбцами равно ширине зазора между двумя рядами отверстий s, между строками — расстоянию между отверстиями l. «Шнурки» идут справа налево от точки 1 до точки 2n, как бы отражаясь в зеркале при переходе c левой стороны на правую, и наоборот. График американского зигзага имеет прямолинейные ветви, он короче двух остальных способов шнуровки.

Сокращенные диаграммы европейской шнуровки и шнуровки с запасом. Из рассмотрения исключены горизонтальные отрезки, поэтому в строке осталось n — 1 отверстий. При «отражении» левых ветвей графиков от горизонтальной прямой, проходящей через их нижние точки, становится очевидным, что шнуровка с запасом длиннее европейской.

‹

›

Открыть в полном размере

Нам известны пять основных способов шнуровать ботинки: так называемый американский зигзаг (который был известен еще до открытия Америки), европейский стандарт, шнуровка с запасом и два варианта канадской затяжки. «Пользователь» ботинок выбирает тот или иной способ, исходя из своих эстетических запросов, удобства и времени, которое требуется для шнуровки. Для производителя обуви наилучшим будет способ, требующий наиболее короткого и, следовательно, самого дешевого шнурка.

Посмотрим, какая длина шнурка оказывается минимально необходимой для всех пяти способов (свободные концы, которые служат для завязывания, принимаются одинаковыми и поэтому из рассмотрения исключаются). Ботиночные отверстия пронумеруем сверху вниз и будем считать их точками, а шнурок — геометрической линией, толщины не имеющей. Введем обозначения:

n — число пар отверстий,

l — расстояние между отверстиями в ряду,

s — ширина зазора между двумя рядами отверстий.

Совершенно очевидно, что шнурки в обоих вариантах канадской затяжки будут иметь одинаковую длину L_k = (n — l)(s + 2l). Она должна быть наименьшей из всех возможных, ибо соединяет все отверстия по кратчайшим расстояниям. Нетрудно рассчитать и длину шнурка для остальных способов шнуровки, воспользовавшись теоремой Пифагора:

Американский зигзаг:

Европейский стандарт:

Шнуровка с запасом:

Какая из этих величии будет наименьшей? Предположим, для простоты, что n = 8 (как и показано на рисунке), l = 2 см, a s = 5 см. Тогда все способы шнуровки дадут нам следующие значения:

канадский

L_K = 7(5+4) = 63cм

американский

европейский

с запасом

Канадская затяжка действительно оказалась самой короткой при любых значениях n, l и s. Но всегда ли из трех оставшихся американский зигзаг дает минимальное значение длины? Методами математического анализа, которые изучают в вузе, можно показать, что если n не меньше 4, американский способ действительно дает наименьшую длину; несколько большей длины требует европейский стандарт, а шнуровка с запасом оказывается наименее «экономной». При n = 3 американский зигзаг по-прежнему оказывается самым коротким, но остальные становятся равными по длине. Если же отверстий только два, все три способа дают одинаковые результаты!

Этот арифметический подход, однако, никак не объясняет, почему разные способы шнуровки требуют разной длины шнурков и почему у американского зигзага она минимальна. Наглядно показать это удастся при помощи геометрии и некоторых физических идей.

В середине XVII века французский математик и физик Пьер Ферма (широко известный благодаря своей знаменитой «великой теореме») установил основной принцип геометрической оптики. В современной формулировке он гласит, что свет всегда распространяется по пути, требующему для преодоления наименьшего времени. Этот принцип, в частности, объясняет законы преломления и отражения света.

Джон Халтон использовал принцип Ферма в своих исследованиях по «ботинкологии». Он составил прямоугольную диаграмму, где по горизонтальным строкам были отложены 2n точек с интервалом s между ними и расстоянием l по вертикали между n строками. Нечетные столбцы диаграммы изображают левый ряд отверстий, четные — правый (с точки зрения хозяина ботинок). Начнем «шнуровать» диаграмму, соединяя линией точки (1,1) и (2n,1) разными способами. При этом всякий раз будем переходить, скажем, от столбца 2 к столбцу 3, от 3 — к 4 и так далее, вместо того, чтобы возвращаться к 1, 2 и опять к 1, как в настоящих ботинках. Это равносильно тому, что каждый столбец как бы играет роль зеркала, в котором по законам геометрической оптики отражаются отрезки шнурка между рядами отверстий. И, согласно тем же законам, отражения имеют ту же длину, что и сами отрезки.

На получившейся диаграмме американский зигзаг предстал в виде трех прямых. Совершенно очевидно, что в сумме они короче ломаных линий, изображающих остальные способы шнуровки. Не столь очевидно, однако, что «европейская» шнуровка короче шнуровки с запасом. Нагляднее всего это можно показать, если выбросить из обоих графиков отрезки, идущие горизонтально. Их n — 1, все они соответствуют кускам шнурка, стягивающим на ботинке правые и левые отверстия в одном ряду, и, следовательно, имеют одинаковую длину s. В результате получатся два V-образных графика. Отразим левые ветви каждого, как в зеркале, в строках, проходящих через нижние их точки. Шнуровке с запасом будет отвечать ломаная линия, а европейскому стандарту — прямая, которая короче любой ломаной. Аналогичным образом при желании можно представить канадскую затяжку и другие, еще более экзотические способы шнуровки, быть может, известные читателям.

Принцип Ферма, положенный Д. Халтоном в основу анализа «ботинкологических» проблем, широко применяется в оптике, геодезии и геометрии, помогая ответить на гораздо более важные вопросы, нежели — почему американский зигзаг требует коротких ботиночных шнурков.

По материалам журнала «Scientific American».

Подробнее см.: https://www.nkj.ru/archive/articles/33437/ (Наука и жизнь, Шнуровка ботинок по принципу Ферма)

Впервые вопросом о самом длинном водном маршруте задался один из пользователей сообщества Reddit под ником kepleronlyknows. Его настоящее имя — Патрик Андерсон(Patrick Anderson), он работает адвокатом, а на досуге пролистывает «Википедию» и рассматривает карты. Андерсон предположил, что путь от южного побережья Пакистана до северо-восточного побережья России — самый длинный путь в океане, который можно проложить по прямой линии. 

Теперь специалисты из Исследовательского центра в Корке (Ирландия) и Исследовательского центра IBM (Индия) рассчитали точную длину маршрута от Аравийского моря до Камчатки: 32 089,7 километра. Это действительно самое длинное путешествие по прямой линии на Земле. Естественно, маршрут гипотетический, поскольку мало кому придет в голову добираться из одной точки земного шара в другую так долго.

Также ученые рассчитали максимально длинный маршрут исключительно по суше. Расстояние по прямой от поселка Сагреш в Западной Португалии до города Цюаньчжоу в Восточном Китае составляет 11 241 километр. На этом маршруте нет крупных водных препятствий, впрочем, модель не учитывает объекты менее 1,8 квадратного километра. Так что путешествовать по этим маршрутам ученые все-таки не рекомендуют.

The geometric figures are not only part of our environment, but are also protagonists of a large part of the architecture we know. In this case, reality is allied to build architectural figures, and transform them into geometric creations.

В 1796 году Карл Фридрих Гаусс, учащийся первого курса Геттингенского университета, решил задачу, перед которой математическая наука пасовала более двух с лишним тысяч лет