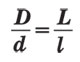| Головна » Статті » Цікава математика |
Кандидаты педагогических наук Марина ЕГУПОВА и Наталья КАРПУШИНА. Мы привыкли доверять своим глазам и не задаёмся вопросом, почему один и тот же объект вблизи выглядит крупнее, чем вдали? Или почему разные по величине предметы порой кажутся одного размера? Механизмы зрения довольно сложны, однако некоторые его особенности можно объяснить на основе геометрических представлений.
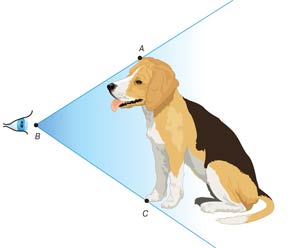
Угловой размер объекта — это угол зрения, под которым виден весь объект (в данном случае — угол АВС).
Измерение высоты светила при помощи посоха Якова.
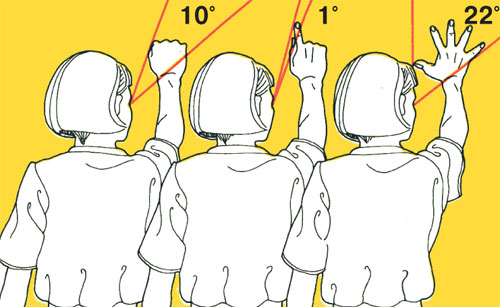
Рука — природный угломер.
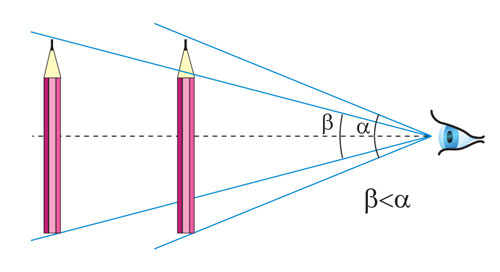
Один и тот же предмет визуально может иметь разные размеры в зависимости от удалённости от глаза наблюдателя.
Изображение предмета на сетчатке глаза получается перевёрнутым вверх ногами (обратным) и уменьшенным.
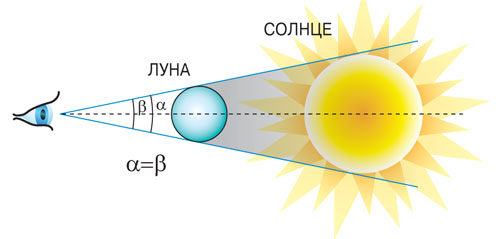
Геометрия полного солнечного затмения.
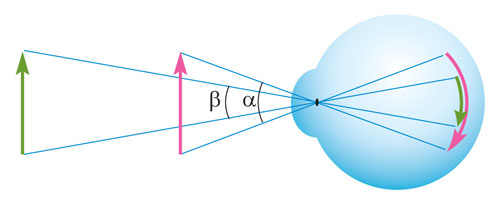
Под одним углом зрения видимые линейные размеры предметов кажутся одинаковыми. ‹ ›
Что такое угол зрения
Всякий предмет имеет линейные размеры: длину, ширину и высоту. Но как только он попадает в наше поле зрения, то приобретает ещё один размер — угловой. Давайте разберёмся, что это означает. Когда мы смотрим на предмет, то через каждую его точку можно провести от глаза луч, называемый лучом зрения. Понятно, что их будет бесконечно много. Любые два луча зрения образуют угол зрения. Тот угол зрения, под которым предмет виден целиком, и принято называть угловым размером предмета. Как и всякий плоский угол, он измеряется в градусах, минутах, секундах или в радианах. Понятие углового размера используется в геометрической оптике, геодезии, астрономии. Встречается оно и в геометрии, но здесь принято говорить об угле зрения, под которым из указанной точки «виден» данный отрезок — высота фигуры, её диаметр и пр. Угловой размер зависит от выбора точки наблюдения, в чём легко убедиться, измерив его из двух точек, расположенных на разном расстоянии от предмета. В зависимости от характера предмета величину угла зрения, под которым он виден, определяют при помощи специальных приборов, например, для измерений на местности используется теодолит, для определения высоты небесных объектов над горизонтом — секстант и т.д. В древности с той же целью применяли более примитивные инструменты. Один из них — посох Якова, предшественник современного секстанта. Он представлял собой стержень, по которому скользила поперечная рейка; на стержень были нанесены деления, соответствующие некоторым углам (их предварительно измеряли транспортиром). Наблюдатель подносил один конец посоха к глазу, другой направлял в сторону измеряемого предмета и затем перемещал рейку до тех пор, пока она одним концом не «коснётся» линии горизонта, а другим — небесного объекта. После этого оставалось только «снять показания» — посмотреть, какому делению на стержне соответствует рейка. Этот удобный и простой инструмент легко изготовить самому, он вполне годится для примерного измерения углов в любой плоскости. Наконец, оценить угловой размер предмета можно буквально «голыми руками». Угломером послужит кисть руки, если, конечно, знать некоторые углы. Например, ноготь указательного пальца вытянутой перед собой руки мы видим под углом, приблизительно равным 1о, кулак — под углом 10о, а промежуток между концами расставленных большого пальца и мизинца — под углом 22о. Угловой размер и расстояние Угловой размер предмета — величина не постоянная и зависит от расстояния предмета от глаза: чем предмет дальше, тем меньше угол зрения, под которым он виден. Чтобы понять причину этого явления, вспомним, что на сетчатке глаза изображение предмета получается обратным и уменьшенным. При удалении предмета его изображение на сетчатке становится меньше, поэтому он и кажется нам уменьшающимся. При сокращении расстояния изображение, напротив, увеличивается и предмет кажется увеличивающимся. На языке геометрии это означает, что величина угла зрения обратно пропорциональна расстоянию до предмета.
Такая особенность зрения помогает понять некоторые наши действия и явления вокруг нас. Почему, например, чтобы рассмотреть детали висящей на стене картины или мелкий шрифт на странице книги, приходится подходить к холсту ближе или подносить текст к глазам. Ответ прост: нам необходимо увеличить изображение на сетчатке, а для этого следует увеличить угол зрения, что мы и делаем, уменьшая расстояние до предмета. Другой пример. Представьте себе две «убегающие» вдаль параллельные линии (железнодорожные рельсы, края прямолинейного шоссе). Они кажутся «сходящимися» в одной точке. Такое же впечатление создают ряды телеграфных столбов или деревьев вдоль дороги. Зрение будто пытается убедить нас в том, что вопреки законам геометрии параллельные прямые пересекаются. Но это лишь иллюзия, которая возникает из-за видимого уменьшения расстояния между прямыми по мере их удаления. Под одним углом зрения Часто приходится сталкиваться и с другой ситуацией. Если рассматривать предметы одинаковой формы, но разных линейных размеров под одним и тем же углом зрения, то кажется, что их размеры равны. Это подтверждает простой опыт. Выстройте по росту несколько матрёшек и по-смотрите на них со стороны самой маленькой фигурки, а затем медленно отойдите назад, не изменяя направления взгляда. Вы увидите, как матрёшки начнут «сливаться», загораживая одна другую. Наконец, когда вы отодвинетесь на некоторое расстояние, будет видна только одна матрёшка — ближайшая к вам. Если теперь сместить фигурки в стороны так, чтобы все они были полностью видны, то визуально матрёшки будут казаться одного размера. Похожее явление можно наблюдать и в природе. Например, при полном солнечном затмении лунный диск в точности заслоняет солнечный. В этот момент наблюдатель с Земли видит оба небесных тела под одним углом зрения. Увидеть такое уникальное явление было бы невозможно, если бы линейные размеры Солнца и Луны, а также расстояния от них до Земли не состояли в определённой математической зависимости. С точки зрения геометрии в обоих случаях мы имеем дело с подобием фигур, точнее говоря, с гомотетией, с центром, совпадающим с глазом наблюдателя. Поэтому, если два схожих по форме предмета видны под одним углом зрения, то их линейные размеры отличаются во столько же раз, во сколько раз отличаются расстояния до предметов. Таким образом, диаметры Солнца и Луны (D и d) и расстояния от этих тел до Земли (L и l ) связаны простой формулой:
Мы раскрыли далеко не все секреты зрения. Особенности зрения, когда человек смотрит двумя глазами, объяснение некоторых зрительных иллюзий, создание зрительных эффектов в архитектуре и живописи — разговор об этом впереди.
| |
| Переглядів: 280 | |
| Всього коментарів: 0 | |